Guía de pasos en Excel

Así como Eviews 7 es una herramienta para el análisis econométrico, en excel también es posible ejecutar y prácticar este tipo de análisis, obteniendo la regresión de las variables necesarias a estudiar, como por ejemplo veremos a continuación:

Se tiene una data en Excel con las variables "X" y "Y", para el cuál "X" es ingreso, "Y" consumo y tienen las siguientes cantidades desde  1991 a 1995:

X = 84, 108, 92, 110, 106
Y = 32, 40, 36, 44, 48

Lo primero consiste en sombrear las variables X y Y para luego ir a "Insertar", seleccionamos "Gráficos" y al aparecernos el cuadro mostrado anteriormente fijamos o damos click en "X Y(Dispersión)", señalando el primer gráfico para luego dar "Aceptar".

Hasta el momento tendremos nuestro gráfico de dispersión el cuál podemos apreciar a continuación:

Es importante agregar una línea de tendencia frente a los puntos de dispersión obtenidos, por lo que daremos click derecho en un punto de dispersión cualquiera y seleccionaremos "Agregar línea de tendencia", se abrirá un cuadro al que remarcaremos en tipo de tendencia o regresión "Lineal" y en la parte inferior señalamos "Presentar ecuación en el gráfico" y "Presentar el valor R cuadrado en el gráfico", luego damos cerrar.

Como parte final se obtuvo la ecuación y el R cuadrado de la relación consumo e ingreso en donde se aprecia que los resultados en Excel son idénticos a los de EViews 7 (elaborado en una clase anteriormente).

Y = -7.6923 + 0.4769X

R^2 = 0.7392

Guía de pasos en EViews 7

Una vez instalado el programa Eviews 7 en el sistema operativo, podremos iniciar su uso mediante la siguiente guía elaborada de forma concreta:

Iniciando en EViews 7

 Una vez puesto en funcionamiento el programa EViews 7, nos aparecerá una ventana como la mostrada a continuación:

Aquí crearemos nuestro primer archivo de trabajo en EViews 7, para el cuál tomaremos como estudio a las variables "consumo" e "ingreso" que casi siempre son utilizadas en la explicación básica de la econometría por su sencillez al momento de ser relacionadas.

Aplicación de los lineamientos de econometría en EViews 7

a)Planteamiento de la teoría económica: Como dijimos un párrafo atrás, estudiaremos el consumo y el ingreso, por lo tanto plantearemos la teoría económica la cuál es sostenida por Keynes, es decir, la teoría del consumo, que explica la relación consumo-ingreso, donde describe que cualquier cambio (sea un aumento) en el ingreso de un consumidor provocará variaciones en su consumo (también de aumento), sea el caso de un bien normal. 

b) Especificación del modelo matemático de la teoría: El modelo matemático para la teoría del consumo de Keynes esta dada de la siguiente manera:

Y=a+bX

Donde:  Y = Consumo

            X = Ingreso

            a = Consumo autónomo (Consumo independientemente de los ingresos)

            b = Propensión marginal a consumir (PMC), ( 0>b=PMC<1)

c) Especificación del modelo econométrico de la teoría: Para que un modelo matemático pase a ser econométrico simplemente se le agrega una variable aleatoria o un error estocástico expresado por "u", donde irán todas las variables que también afectan al consumo pero que por distintos motivos no fueron tomadas. De esta forma nuestro modelo econométrico será el siguiente:

Y=a+bX+u 

Donde:  Y= Variable endógena o dependiente.

            X= Variable exógena o independiente.

            a,b = parámetros o estimadores.

            u = error estocástico o residuo.

d) Recopilación de datos: usaremos una base de datos con información anual, muy sencilla para la demostración necesaria, así como se muestra en el siguiente cuadro, donde "Y" es consumo y "X" ingreso como se mencionó anteriormente: 

e) Estimación de los parámetros del modelo econométrico: Para este paso iniciamos el manejo del programa EViews 7, donde arrancamos con el primer paso, como se muestra en la siguiente imagen, seleccionado "File" - "New" - "Workfile".

ya que nuestra base es de forma anual seleccionamos "Annual" en la especificación de la frecuencia (Frecuency):

debajo de Frequency nos encontraremos con dos nuevos casilleros "Start date" y "End date" donde irán los años de la base de datos, en este caso 1901 y 1905 respectivamente, para luego dar OK:

EViews 7 creará un archivo sin nombre alguno, donde apreciaremos también "Range" que es el número total de observaciones y "Sample" que muestra el número de observaciones que están siendo utilizadas. Ambos son iguales cuando se crea un archivo, pero si más adelante se desea utilizar una muestra mas pequeña se modificará "Sample".

posteriormente guardaremos el archivo, de la misma forma que se sabe guardar cualquier otro archivo. Seleccionamos "File" - "Save" ...

 

seguimos con la importación de datos que puede ser elaborado de las siguientes formas:

Primera forma de importar datos:

Seleccionamos "File" - "Import" - "Read"

buscamos la base de datos a importar dentro de nuestros archivos, que se encontrará como formato excel, para abrirlo:

aparecerá un cuadro donde colocaremos el nombre de las variables, que son Y (consumo) y X (ingreso), separados de un espacio y damos OK.

Segunda forma de importar datos: (Es necesario darle un vistazo a ésta forma ya que aquí aprenderemos a hacer grupos en EViews 7)

Simplemente copiamos la data desde excel, pero para eso iniciamos creando las series "Y" y "X" . seleccionado "Object" - "New object" 

Pasamos a seleccionar "Series" y a darle nombre el nombre de la variable, en este caso "Y" y presionamos OK, posteriormente realizamos los mismos pasos desde "Object" - "New object" - "Series" y creamos la Serie para la variable "X".(Lo mismo se hará en caso de presentarse más variables)

Aparecerán ambas series con sus respectivos nombres, los cuáles abriremos como grupo seleccionando cada una d ellas teniendo presionado la tecla "Ctrl" (control), una vez sombreadas ambas series hacemos click derecho sobre éstas y señalamos "Open" - "as group"

 y tendremos las series "Y", "X" juntas como un grupo, en donde notaremos NA, ya que aún no se ha colocado dato alguno.

para que aparezcan los valores dentro del grupo debemos abrir nuestra base de datos en excel y copiar las celdas (es ideal que nuestro grupo haya sido abierto en el mismo orden que se presentan las variables en Excel, es decir primero "Y" y luego "X")

Luego vamos a EViews 7, y presionamos "Edit +/-" para que se permita pegar los valores copiados anteriormente:

Nos ubicamos en la primera celda de la ventana de Eviews 7, hacemos click derecho para seleccionar "Paste", y se habrá terminado de ingresar los datos. 

No es necesario guardar el grupo al momento de cerrar

Hasta aquí ya se ha logrado importar los datos recopilados en nuestro Excel, y hemos aprendido a crear grupos, ya con ésto podemos realizar gráficos en nuestras variables.

Abrimos como grupo las variables "X" y "Y" para luego seleccionar "View" - "Graph..."

Seleccionamos "Scatter" que viene a ser la dispersión, y "Regression Line" que es la regresión lineal y presionamos OK.

Nuestro gráfico será el siguiente:

En nuestro gráfico es ideal usar la regresión lineal, para tener un alcance a la vista de la distancia entre la dispersión ,es decir la nube de puntos y su media, que se puede denotar como la línea roja.

Para guardar el gráfico simplemente presionamos "Name", nos aparecerá un cuadro donde colocaremos el nombre, y una vez puesto damos OK.

pero ¿a donde queremos llegar?, lo que deseamos es la estimación de los parámetros de nuestro modelo econométrico(Y=a+bX+u), y es posible realizarse mediante el método de los "Mínimos Cuadrados Ordinarios" que nos ayuda a encontrar los mejores estimadores lineales insesgados, es decir, que el valor esperado de estos estimadores serán iguales al verdadero valor.

En Eviews 7 lo lograríamos con los siguientes pasos:

Primero: Seleccionamos "Object" - "New Object" - "Equation" - "OK", o también podríamos hacer "Quick" - "Estimate equation"; ambas formas nos llevan a la misma ventana e indicaremos el nombre de las variables dentro del primer recuadro, que serán Y C X, separadas de un espacio una de la otra, "C" es la constante que cumple el valor de "a".

Luego en la parte inferior elegimos el Método que será "LS - Least Squares(NLS and ARMA)" y finalmente aceptar.

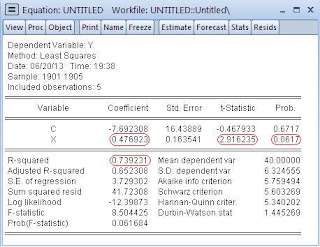
y el resultado de nuestra regresión será: "Y= -7.692308 + 0.476923X + u"

Como interpretación del cuadro anterior podemos señalar que cuando hay un aumento en el INGRESO(X) de un consumidor en 1$, el CONSUMO(Y) aumentará en 0.476923$, así también según el R - Squared o R^2( R cuadrado) la variable Y (consumo) es explicada en un 73.9231% por la variable X (ingreso).

f) Prueba de Hipótesis: La prueba de hipótesis con el "Prob(p)" es la siguiente:

   H0: "b" sea igual a cero

   H1: "b" sea diferente de cero

Si p < 0.05, rechazamos H0 y aceptamos H1 -----> Significativo

Si p > 0.05, no rechazamos H0 y rechazamos H1  ------> No significativo

En el caso anterior podemos observar q nuestro Prob(p) del estimador "b" es 0.0617, es mayor que 0.05, por lo que no rechazamos H0, y en conclusión el modelo al pasar por la prueba de hipótesis es no significativo.

g) Predicción:  La predicción es un pronóstico acerca del posible comportamiento de las variables, y se realiza mediante el uso de un modelo de regresión o ecuación, la cuál debe ser claramente significativa por las pruebas de hipótesis. En el caso elaborado anteriormente el modelo resulto ser no significativo, ya que este ejemplo no tiene como fin hacer predicciones sino detallar una guía para el trabajo en EViews 7, por lo que se aprecia una data muy sencilla y escasa a la vez.

h) Implicancia de la predicción para la aplicación de política económica: Otro punto importante después de conocer los estimadores de un modelo y otorgando su validez, es la alternativa que nos ofrece para la toma de decisiones dentro de la política económica, ya que  conocemos el comportamiento de las variables y nos facilitan la interpretación de muchos cambios, por lo que son necesarias como herramientas, que en ningún tiempo podrán sustituir a la verdadera experiencia.

Multicolinealidad

La multicolinealidad es una violación de los supuestos del modelo clásico de regresión, que se da por la existencia de una correlación entre las variables exógenas, también denominadas independientes o regresoras. 

Podemos hablar de multicolinealidad perfecta, cuando los estimadores de la regresión son indeterminados, es decir, no pueden ser hallados; a diferencia de la multicolinealidad menos que perfecta, en la que si es posible hallar el estimador "B".

Por la existencia de multicolinealidad no significa que los estimadores MCO dejen de ser MELI, pero si conllevan a tener varianzas y covarianzas muy altas.

La multicolinealidad aparece cuando el modelo no fue correctamente especificado o hay redundancia entre las variables, así como también el problema puede provenir desde el recojo de información.

Como mencionamos anteriormente, cuando se tiene un caso de multicolinealidad perfecta no es posible hacer la regresión por el simple hecho de no poder hallar el estimador "B", pero cuando estamos frente a una multicolinealidad menos que perfecta si sería posible, pero ¿ Cómo podemos detectar que estamos en un caso como éste?; la multicolinealidad menos que perfecta, se caracteriza por mostrar resultados en una regresión como R^2 muy altos y al mismo tiempo sus variables al pasar por la prueba de hipótesis de forma individual son no significativas, y si tratamos de correlacionar ambas variables exógenas o regresoras entre pares, tendremos también un coeficiente de correlación muy alto, cercano a uno.

Sea el caso mostrado en el cuadro se aprecia claramente un R^2 muy alto, es decir, que la variable "Cons" es explicada en 80.3625% por las variables "Y" e "IMP1", mientras que éstas mismas son variables no significativas, siendo evaluadas de forma individual, ya que su p>0.05.


La mejor forma de terminar con la multicolinealidad es eliminando una de las variables exógenas que se viene correlacionando con la otra.

Teorema de Gauss Markov

El teorema de Gauss Markov señala que los estimadores de MCO (Mínimos Cuadrados Ordinarios), es decir, los "B"; presentan una varianza mínima, lo que hace de ellos los más eficientes. También son aquellos pertenecientes a la familia de estimadores insesgados.

Los estimadores MCO son conocidos como MELI, que significa Mejores Estimadores Lineales e Insesgados.

Se expresan de la siguiente forma:

LINEALIDAD: 

INSESGADEZ:

EFICIENCIA:

Al referirnos que los estimadores "B" tienen varianza mínima, podemos decir de la forma más simple, que presentan el menor error cuadrático comparado a otros estimadores, y hace por ello que sean los más eficientes, todo esto con el fin de que la función de regresión muestral sea lo más cercana posible a la función de regresión poblacional, por lo que podemos hablar de insesgadez.

Supuestos del modelo clásico de regresión lineal

Es importante tener muy en cuenta los siguientes supuestos:

1) Linealidad en los parámetros:

 Este supuesto indica la necesidad de que los coeficientes sean lineales, es decir, que sus exponentes o potencias sean 1.

Y = B₀ + B₁X₁ + B₂X₂ + B₃X₃ + … + u

Algo resaltante en este supuesto es la linealidad en los parámetros, que es muy distinto a expresar una relación lineal entre las variables "X" y "Y".


2) Condición de rango: 

Es un supuesto de confirmación e identificación, que nos indica si es posible hallar el estimador "B".

Rango(X) = K

Dentro de este supuesto se debe cumplir:

- Las columnas de la variable X deben ser linealmente independientes.
- No debe existir multicolinealidad, es decir relaciones lineales entre las variables         independientes o exógenas.
- El número de observaciones debe ser mayor que el de variables exógenas, n < k


3) La media condicional de "u" dado "x" es cero: 

Se tiene como primer momento que las perturbaciones presentan media incondicional nula. 

E [u | x] = 0   =>   E [u_i] = 0  ,   i = 1, 2, … , n

La media condicional de U dado X es cero, es decir la covarianza entre U y X debe ser nula. Se interpreta como la NO influencia de "u" en la variable independiente o exógena, o por decirlo así "u" explica en cero a la parte determinística.

     E [u | x] = 0    =>    E [x´u] = 0    =>   Cov (x,u) = 0

4) Homocedasticidad y No autocorrelación:

Dentro de este punto podemos resaltar dos supuestos muy importantes:

La homocedasticidad o no heterocedasticidad, es el segundo momento condicional donde la varianza de cada perturbación u_i es constante o se mantiene igual para todas las observaciones.   

Var [u | x] = ơ² I

La No Autocorrelacion, muestra que las perturbaciones u_i y u_j no están correlacionadas entre sí. Forman el primer momento cruzado condicional de las perturbaciones que es cero.

E [u_i, u_j | x] = 0    =>   COV [u_i, u_j | x] = 0    

* Donde i,j son diferentes

Correlación

La correlación o coeficiente de correlación se encarga de medir el grado de relación o dependencia lineal entre dos variables, determinando si el cambio de una afecta a la otra. En el hecho que ocurra, podremos decir que existe correlación entre ambas.


El coeficiente de correlación también se muestra como "r"

Traduciendo la siguiente fórmula decimos que:

El Coeficiente de correlación "r" es igual a la covarianza de "xy" entre el producto de la varianza de "x" y la varianza de "y".


Los valores que puede tomar el coeficiente de correlación "r" son entre -1 y 1 (-1 < r < 1)


Si "r" > 0, existe una correlación lineal positiva, es decir, si aumenta el valor de una variable, lo mismo pasará con la otra. La correlación lineal positiva es mayor mientras más se aproxima a 1.

Si "r" < 0, existe una correlación lineal negativa, es decir, si incrementa el valor de una variable, disminuirá el valor de la otra. La correlación lineal negativa es más fuerte cuando se aproxima a -1.

Si "r" = 0, no existe correlación lineal entre ambas variables.

Si r = 1 ó -1, los puntos de la nube se ajustan o están sobre la recta creciente o decreciente. Entre ambas variables hay dependencia funcional.

Introducción a la Econometría

Podemos deducir rápidamente un concepto general de Econometría, como la medición económica; por el simple hecho en el que está conformada esta palabra, es decir, "econo" "metría"; que sin lugar a duda nos muestra un mejor panorama de lo que encontraremos dentro de esta disciplina. ¿Pero que puede ser medición? y ¿que vamos a medir en la economía?. La medición consiste en la aplicación de la estadística matemática a la información económica. Pero sin un fin nada tendría sentido, es por eso que la econometría utiliza la estadística matemática para dar un sustento aplicado en la realidad a cualquier modelo creado por la economía.

El uso de la econometría nos permitirá formular hipótesis de forma cuantitativa, es decir se obtendrán resultados numéricos, con el que podemos comprobar empíricamente (aplicado a la realidad) a la teoría económica, la cuál presenta naturaleza cualitativa. Para esto se utilizarán las ecuaciones matemáticas, en la que se relacionará una variable "dependiente"(endógena) con una o más variables "independientes"(exógenas), conocidas generalmente por "Y" y "X" respectivamente.

Las variables "X" y "Y" son conocidas de muchas formas, es por esto que a continuación veremos una serie de nombres más utilizados para ellas.

Variable Y: Es la variable dependiente, endógena, explicada o regresada.
Variable X: Es la variable independiente, exógena, explicativa o regresora.


La metodología tradicional de la Econometría se desenvuelve mediante los siguientes lineamientos:

a) Planteamiento de la teoría económica
b) Especificación del modelo matemático de la teoría
c) Especificación del modelo econométrico de la teoría
d) Recopilación de datos
e) Estimación de los parámetros del modelo econométrico
f) Prueba de hipótesis
g) Predicción
h) Implicancia de la predicción para la aplicación de política económica.

Existen muchas herramientas para la Econometría, paquetes informáticos especializados para el trabajo dentro de estos lineamientos. El eviews 7 es uno de ellos, el cuál utilizaremos para la elaboración de modelos econométricos los cuáles serán contrastados con la realidad e interpretados para comprobar su validez de acuerdo a la teoría económica.